Kodatuno User's Guide	Prev Index Next

---

（Ex．6）等高線を生成する

　等高線は3次元空間上の曲面における，ある方向の値が等しい点の集合です．これを求めるということは，言い換えれば， 曲面と平面の干渉線を求めているということになります．

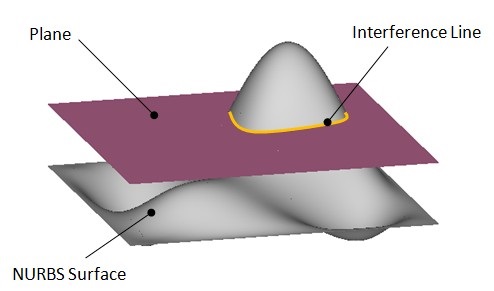　本例題では，図に示すように，Z方向に平面をZ_minからZ_maxまであるシフト量Dでシフトしていきながら，それぞれの等高線 を求めていきます． ここで，"等高線"と言っていますが，実際には点群によって表現しています． "SampleFunc2.cpp"の SmpContourLine()を実行します．

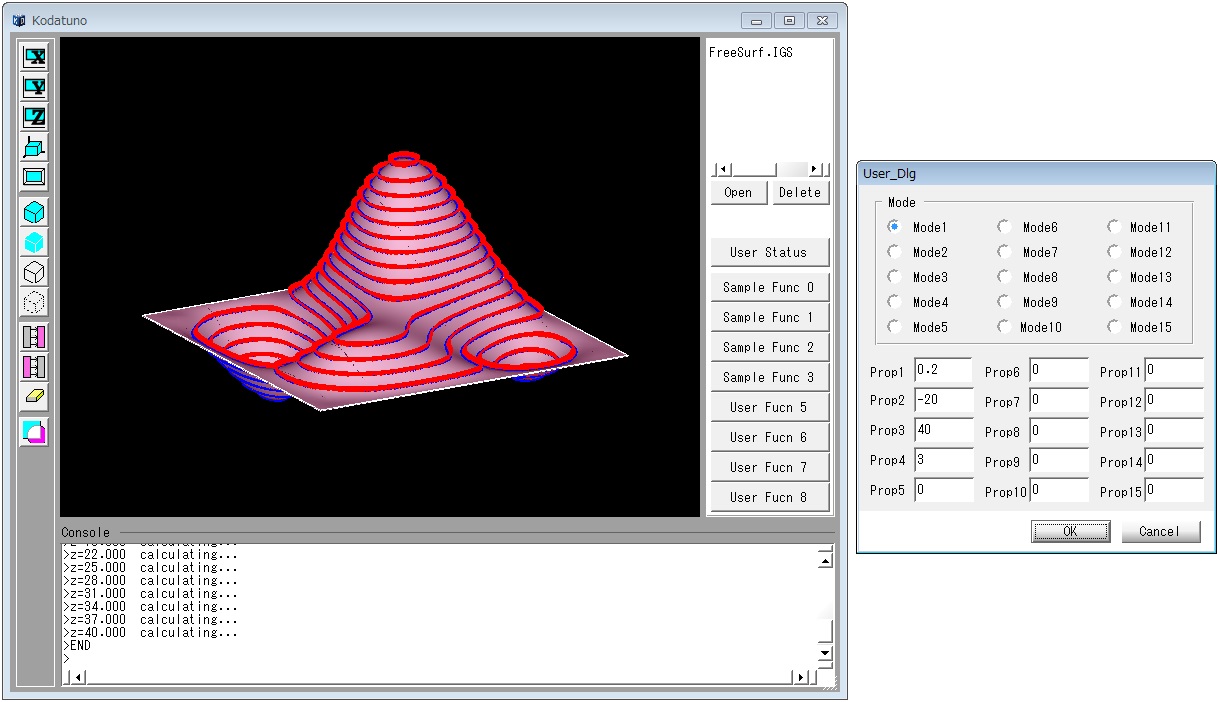
＜実行手順＞

1. Kodatunoアプリケーションを起動し，適当なIGESデータを1つ読み込みます．
2. 表示されたBodyから面をピックします．ピックする面の数は1個にしてください．
3. "User Status"からMode1を選択し，Prop1に交点群の点間隔(0.1〜2程度)，Prop2にZ_min, Prop3にZ_max, Prop4に平面のシフト量Dを入力します．
4. "Sample Func 2"ボタンを押します．
5. 選択した面上に等高線が生成されたことを確認してください．

＜ソース解説＞

　今回はユーザー用ボタンの3つ目，"Sample Func 2"を押したことに注意してください．これによって"UserFunc.cpp"のUSER クラスのコンストラクタのExecSampleFunc2()が実行される ことになります．

// Sample5: 曲面のUVパラメータで等間隔に分割した点を生成する
int SmpUVDivLine(BODYList *BodyList,OBJECTList *ObjList, int PickCount, double Prop[])
{
	if(!PickCount)	return KOD_ERR;		// セレクションされていなかったら、何もしない

	NURBS_Func	nfunc;					// NURBSを扱う関数集を呼び出す
	double green[3] = {0,1,0};			// 点表示の色(緑)

	OBJECT *obj = (OBJECT *)ObjList->getData(0);		// 一番最初にセレクションされたエンティティの情報を得る
	BODY *body = (BODY *)BodyList->getData(obj->Body);	// 一番最初にセレクションされたBODYの実体を得る

	// 本来であれば，Sample4に示した曲面のタイプによる条件分岐が必要であるが，これ以降のSampleではトリム面で決め打ちする
	if(obj->Type != _TRIMMED_SURFACE)	return KOD_ERR;	

	NURBSS *S = body->TrmS[obj->Num].pts;				// BODYからNURBS曲面を取り出す

	int u_divnum = (int)Prop[0];						// ユーザーステータスのprop1をu方向分割数として読み込み
	int v_divnum = (int)Prop[1];						// ユーザーステータスのprop2をv方向分割数として読み込み
	double u_val = (S->U[1] - S->U[0])/u_divnum;		// パラメトリック空間内でのu方向線分長を得る
	double v_val = (S->V[1] - S->V[0])/v_divnum;		// パラメトリック空間内でのv方向線分長を得る

	// u方向，v方向の各分割点における座標値を求める
	for(int i=0;i<=u_divnum;i++){
		for(int j=0;j<=v_divnum;j++){
			Coord P = nfunc.CalcNurbsSCoord(S,S->U[0]+u_val*i,S->V[0]+v_val*j);	// 指定した(u,v)の座標値を求める
			DrawPoint(P,1,3,green);						// 描画
		}
	}

	return KOD_TRUE;
}

　Mode1を選択したので，UserStat.Modeには0が代入されており，6行目のSpmContorLine()が実行されることになります．
　では，SmpContourLine()を見てみましょう．SmpContourLine()は"SampleFunc2.cpp"に記述されています．

// Sample6: 等高線を生成する
// 具体的には，NURBS曲面と平面との交線(交点群)をZ方向に順次求めていく
// さらに，その交点群の法線ベクトルも算出する
int SmpContourLine(BODYList *BodyList,OBJECTList *ObjList, int PickCount, double Prop[])
{
	if(!PickCount)	return KOD_ERR;		// セレクションされていなかったら、何もしない

	clock_t start,end;
	start = clock();

	NURBS_Func	nfunc;					// NURBSを扱う関数集を呼び出す

	OBJECT *obj = (OBJECT *)ObjList->getData(0);		// 一番最初にセレクションされたエンティティの情報を得る
	BODY *body = (BODY *)BodyList->getData(obj->Body);	// 一番最初にセレクションされたBODYの実体を得る
	if(obj->Type != _TRIMMED_SURFACE)	return KOD_ERR;	// セレクションされた曲面がトリム面でない場合は終了

	NURBSS *S = body->TrmS[obj->Num].pts;				// BODYからNURBS曲面を取り出す

	Coord t[5000];					// 解格用納
	double red[3] = {1,1,0};		// 法線ベクトル表示の色
	double blue[3] = {0,0,1};		// 点表示の色
	char mes[256];					// メッセージ出力用

	double feed = 0.2;//Prop[0];			// 交点群の点間隔
	double under = 0.01;//Prop[1];			// 等高線のZ_min
	double upper = 100;//Prop[2];			// 等高線のZ_max
	double delta = 1;//Prop[3];			// 等高線生成のZ間隔
	int step = fabs(upper - under)/delta + 1;	// 等高線の本数を算出

	Coord nvec = SetCoord(0,0,1);	// 平面の法線ベクトルを指定(X-Y平面とする)

	// 平面をZ方向にシフトしていきながら，等高線を算出する
	for(int i=0;i< step;i++){
		double z = under + delta*(double)i;	// 現在の平面のZ位置
		Coord pt = SetCoord(0,0,z);			// 現在の平面上の1点を指定

		sprintf(mes,"z=%.3lf  calculating...",z);
		GuiIF.SetMessage(mes);

		int num = nfunc.CalcIntersecPtsPlaneSearch(S,pt,nvec,feed,3,t,5000,RUNGE_KUTTA);		// NURBS曲面と平面との交点群を交線追跡法で求める

		for(int i=1;i< num;i++){		// 交点の数だけループ
			Coord p = nfunc.CalcNurbsSCoord(S,t[i].x,t[i].y);			// 交点をパラメータ値から座標値へ変換
			Coord p_ = nfunc.CalcNurbsSCoord(S,t[i-1].x,t[i-1].y);
			//Coord nt = nfunc.CalcNormVecOnNurbsS(S,t[i].x,t[i].y);		// 交点上の法線ベクトルを計算
			//nt = MulCoord(nt,-2);											// 外向き法線ベクトルへ変換し適当な長さにする
			if(CalcDistance(p,p_) < 1)
				DrawLine(p_,p,3,red);
			//DrawPoint(p,1,3,red);			// 交点を描画
			//DrawVector(p,nt,1,1,red);		// 法線ベクトルを描画
		}
	}
	GuiIF.SetMessage("END");

	fprintf(stderr,"all step num = %d\n",step);
	end = clock();
	fprintf(stderr,"%.2f sec\n",(double)(end-start)/CLOCKS_PER_SEC);

	return KOD_TRUE;
}

　6〜22行目まではこれまでの例題と同じですので，説明を省略します．19行目のCoord　t[5000]は，等高線として得られた 点群を格納するための箱として用意しています．
　24〜27行目では，今回は4つのプロパティ値を入力しましたので，それらを取り出しています．28行目では平面をシフト させる回数を計算しています． NURBS曲面と平面との交点群を算出する関数は40行目のNURBS_Func::CalcIntersecPtsPlaneSearch() によって行われます．この関数に平面の情報を引数として与える必要が あります．平面を定義する方法はいくつかありますが， ここでは平面上の1点ptとその平面の法線ベクトルnvecによって定義し，この2つのパラメータを引数にします． 今回はX-Y平面に 平行な面つまり，平面の法線ベクトルはZ方向に等しいことになりますので，30行目に示すように，nvecに(0,0,1)というベクトルを 与えます． 平面上の1点ptは現在の平面のZ値を与えればよいので，34, 35行目の計算によって与えることができます．
　40行目のNURBS_Func::CalcIntersecPtsPlaneSearch()によって算出された交点群は，引数として与えたtに格納され，その点数は 返値として受け取ります． ここで注意しなければならないことは，交点群はパラメータ(u, v)として(t.x, t.y)に格納される というところです．よって3次元空間上の点にするには，NURBS_Func::CalcNurbsSCoord()を 用いる必要があります(43行目)．
　また本例題では，おまけとして各交点における法線ベクトルを44行目で算出しています．交点，法線ベクトルは，ともに赤色で 表示しています(46, 47行目)．

　以上で(Ex. 6)の解説を終了します．次はNURBS曲面同士の交線算出を行います．