Kodatuno User's Guide	Prev Index Next

---

(Ex. 9) いいかげんな3xCAMの作成

　これが最後の例題になります．最後は，これまでの例題の総括として簡単な（いいかげんな）3xCAMを作ってみたのでご紹介します．

＜実行手順＞

1. Kodatunoアプリケーションを起動し, 適当なIGESデータを1つ読み込みます．
2. 表示されたBodyから面->エッジの順で1つずつピックします．
3. "User Status"からMode4を選択し，Prop1にボールエンドミル半径，Prop2にスキャニングライン分割数(< 100)，Prop3に素材上面のZ座標，Prop4にZ方向分割数（粗加工用）をそれぞれ入力します．
4. "Sample Func 3"ボタンを押します．
5. スキャニングパスが生成されたことを確認してください．

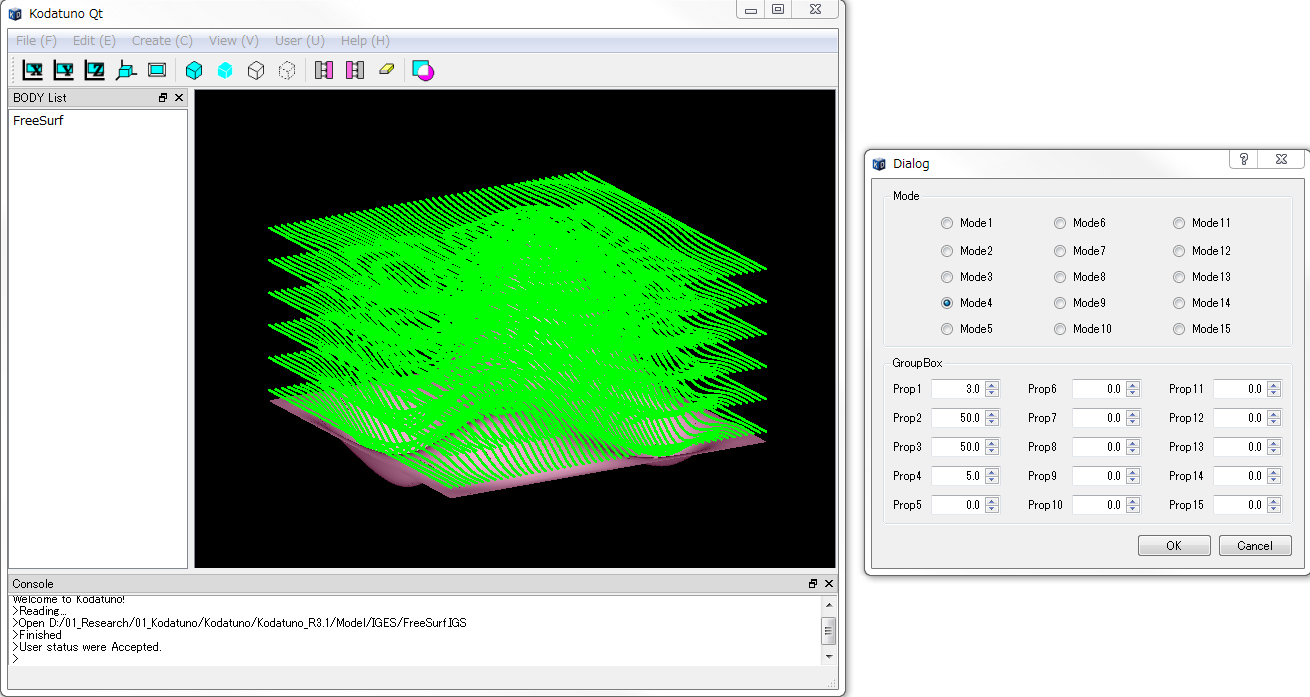
＜ソース解説＞

　今回はModeは関係なく，"Sample Func4"ボタンを押しました．これによってExecSampleFunc3()-->Smp3xCAM()が実行されます．
　では，Smp3xCAM()を見てみましょう．

// Sample9: スキャンパスを生成するシンプルな3xCAM
void Smp3xCAM(NURBSS *S,NURBSC *C,double R,int N,double H,int D)
{
    NURBS_Func	nf;                 // NURBS_Funcへのインスタンス
    double green[3] = {0,1,0};      // 描画するパスの色（緑）
    Coord plane_pt;                 // 分割する平面上の1点
    Coord plane_n;                  // 分割する平面の法線ベクトル
    Coord path_[2000];              // 一時格納用バッファ
    Coord ***path = NewCoord3(D+1,N+1,2000);    // 生成されたパスを格納
    int ptnum[100];                 // スキャンライン1本ごとの加工点数を格納
    int flag = 0;                   // ジグザグパス生成時の方向転換用フラグ

    // ガイドカーブに沿って垂直平面をシフトしていき，加工面との交点群を求めていく
	for(int i=0;i<=N;i++){
        double t = (double)i/(double)N;
		if(i==0) t += 0.0001;		// 特異点回避
		else if(i==N) t-= 0.0001;	// 特異点回避
        plane_pt = nf.CalcNurbsCCoord(C,t);     // 注目中の垂直平面上の1点
        plane_n = nf.CalcTanVecOnNurbsC(C,t);   // 注目中の垂直平面の法線ベクトル
        ptnum[i] = nf.CalcIntersecPtsPlaneSearch(S,plane_pt,plane_n,0.5,3,path_,2000,RUNGE_KUTTA);  // 交点群算出
		// 得られた交点群を，加工面法線方向に工具半径分オフセットさせた点を得る
		for(int j=0;j< ptnum[i];j++){
		 	Coord pt = nf.CalcNurbsSCoord(S,path_[j].x,path_[j].y);     // 工具コンタクト点
            Coord n = nf.CalcNormVecOnNurbsS(S,path_[j].x,path_[j].y);  // 法線ベクトル
            if(n.z < 0)	n = n*(-1);         // 法線ベクトルの向き調整
			path[D][i][j] = pt + n*R;		// 工具半径オフセット
		}
	}

	// 粗加工パス生成
	for(int i=0;i< D;i++){
		for(int j=0;j< N+1;j++){
			for(int k=0;k< ptnum[j];k++){
				double del = (H - path[D][j][k].z)/(double)D;
				double Z = H - del*(double)i;
				path[i][j][k] = SetCoord(path[D][j][k].x,path[D][j][k].y,Z);
			}
		}
	}

	// path描画
	for(int i=0;i< D+1;i++){
		for(int j=0;j< N+1;j++){
			for(int k=0;k< ptnum[j];k++){
				DrawPoint(path[i][j][k],1,1,green);
			}
		}
	}

    // NCコード生成(各条件は各自で変更ください)
	double ret = H + 10;		// リトラクトZ
	FILE *fp = fopen("demo.nc","w");
	fprintf(fp,"G92X0.0Y0.0Z0.0\n");
	fprintf(fp,"S4000M03\n");
	fprintf(fp,"F500\n");
	for(int i=0;i< D+1;i++){
		fprintf(fp,"G00X%.2lfY%.2lfZ%.2lf\n",path[i][0][0].x,path[i][0][0].y,ret);
		for(int j=0;j< N+1;j++){
			if(flag == 0){
				for(int k=0;k< ptnum[j];k++){
					fprintf(fp,"G01X%.2lfY%.2lfZ%.2lf\n",path[i][j][k].x,path[i][j][k].y,path[i][j][k].z);
				}
			}
			else{
				for(int k=ptnum[j]-1;k >=0;k--){
					fprintf(fp,"G01X%.2lfY%.2lfZ%.2lf\n",path[i][j][k].x,path[i][j][k].y,path[i][j][k].z);
				}
			}
			flag = 1 - flag;
		}
		fprintf(fp,"G01Z%.2lf\n",ret);
	}
	fprintf(fp,"G01Z%.2lf\n",ret);
	fprintf(fp,"M05\n");
	fprintf(fp,"M30\n");

	fclose(fp);
}

　基本的には「平面と曲面との交線算出」と「曲面上の法線算出」の組み合わせで事足りてしまいます（14〜28行目）．それ以降の，どのような工具経路とするかはあなた次第！
この例では2番目にピックした曲線をガイドカーブとして，それに沿う形でジグザグパスを生成しています．相対パス上に"demo.nc"が正しく生成されていることを確認してみてください．

　以上で例題は全て終わりです．次のセクションはこれまでの経験を生かして，簡単なアプリケーションを自分で作ってみる練習問題になっていますので，ぜひお試しください．